数控技术发展下，重载机械式主轴系统关键技术受重视

重载机械主轴那可是相当重要的东西，它的有限元建模及模态分析更是主轴动态特性分析里特别重要的一部分，而且还是进一步做动力学分析的基础！这事可争议不了，价值老高了，要是弄不好那后续对主轴的理解和运用啥的都得有问题。

研究基础与发现

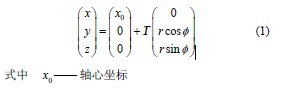
罗筱英等人在这个领域那可是做了不少研究，人家研究了结构参数对砂轮主轴系统动态性能的影响。他们发现支撑刚度对模态影响可大，刚度要是增加，能让第一阶固有频率大幅度提升。不过支撑跨距对模态的影响就相对小多了。这就给咱后续研究指明了一些方向

有限元划分工作

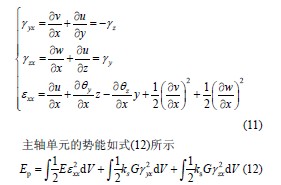
在有限元软件里，还做了关键的划分工作。有人把主轴分别用实体单元和梁单元进行划分，轴承则用Combin14 弹簧单元划分。还以自由模态和实际工况约束条件，进行多约束状态下重载机械式主轴的模态分析，这一步骤很繁杂但是又特别必要

本文聚焦研究

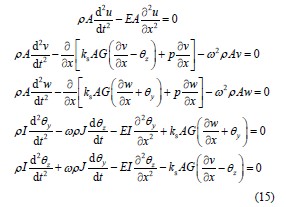
咱们这文主要聚焦多约束状态下主轴的有限元建模、模态分析和试验。像轴向力及转速的影响就没考虑，所以式(18)变成了那样。在把主轴划分为梁单元的分析过程中，还能直接把轴承的刚度系数考虑进来，这种方法挺巧妙的。

多种模态分析情况

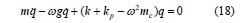
之后分析了好多不同状况下的模态分析。基于Timoshenko 梁有主轴固有频率的计算齿轮刚度计算及其有限元分析proe，还有自由状态下主轴实体模态分析、节点约束的主轴实体模态分析，自由状态和节点约束的 Beam188 梁单元主轴模态分析齿轮刚度计算及其有限元分析proe，弹簧单元约束下Beam188 梁单元主轴模态分析这么多种情况。

不同条件下的频率情况

在完全自由状态下，不对主轴施加任何约束，做了模态分析，前6 阶频率都列出来了。自由状态把它简化为梁单元时也是做的模态分析，前6 阶是刚体模态频率为零，从第7 阶开始的前6 阶频率也有统计。施加约束求解、施加弹簧刚度求解后相关前6 阶频率都展示出来了，还附带振型图。

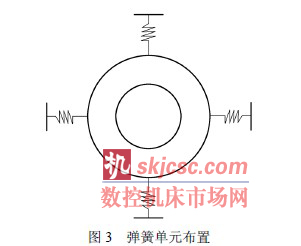
计算结果说明

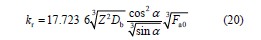
从计算结果看，主轴划分为梁单元时，Timoshenko 梁单元和Beam188 梁单元自由状态下一阶频率误差不大，只是Timoshenko 梁计算结果偏高。对于短粗的主轴结构，用具有剪切效应的Timoshenko 梁或Beam188 单元计算更准。没试验时，用这两种方法去计算有限元建模和进行模态分析得到的结果更准，弹簧约束梁的情况更贴近实际。

大家觉得在实际操作中除了这里研究的因素，还有啥可能影响主轴模态分析结果？要是您觉得本文有点价值，就点赞分享一下！